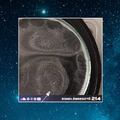
Amikor a nyolcvanas években a Voyager-űrszondák először repültek el a Szaturnusz közelében úgy, hogy rálássanak annak északi sarkvidékére (a korábbi Pioneer-11 küldetésen erre nem nyílt lehetőség) valami döbbenetest vettek észre: egy teljesen szabályosnak tűnő, a környezetétől színében is markánsan elkülönülő óriási hatszög alakú foltot. A mintázat átmérője a becslések alapján közel 30 000 km-esnek adódott, vagyis a hatszög egyetlen oldala hosszabb, mint a Föld átmérője. Nyilván azonnal felmerült az ötlet, hogy a Polar Hexagon (sarki hatszög) nem más, mint egy földönkívüli civilizáció gigantikus bolygómérnöki alkotása, ám a természet is bővelkedik hatszöges szimmetriájú alakzatokban: gondoljunk a hópelyhekre, a méhkaptárak szerkezetére vagy a badacsonyi bazaltorgonákra. Habár az 1997-ben felbocsátott Cassini orbiter nagyon alaposan feltérképezte azóta a Naprendszer legnagyobb légörvényének bizonyuló hatszöget, máig nincsen egyetértés a kutatók között annak tekintetében, hogy mi is okozza e különleges jelenséget. Kollégáimmal a Kármán-laborban gondoltunk egy nagyot és az ESA pályázatára terveztünk egy űrkísérletet, melyben lekicsinyítve modellezhetjük a Szaturnusz óriási hatszögét. Ehhez ráadásul nem is kell elrepülnünk a Naprendszer hatodik bolygójához, elég "csak" kétszázhatvan kilométerrel a harmadik planéta felszíne fölé emelkedni. Erről a tervről szólt a százharmincadik Sokolébresztő.

A DiRoS (Differential Rotation on a Sphere, differenciális forgás egy gömbön) névre keresztelt projektjavaslat célja leegyszerűsítve annyi, hogy egy nagyjából arasznyi, súlytalanul lebegő vízgolyót pörgessünk meg. De úgy, hogy a mikrogravitációban gömb alakot felvenni törekvő vízcsepp "egyenlítői" részét bírjuk rá arra, hogy lényegesen gyorsabban forogjon a tengelye körül, mint a "sarkvidéki" része. A forgási szögsebesség ilyen különbségeit nevezzük egy bolygótest esetében differenciális forgásnak, melyre mind a Szaturnusz, mind az óriási Jupiter, sőt maga a Nap is kitűnő példát szolgáltat kozmikus környezetünkben. Mivel ezen égi objektumoknak nincsen értelmezhető szilárd felszínük, forgásidejüket leginkább épp légköri mintázataik körbeérése alapján becsülhetjük meg. Így tehát azt is mondhatjuk, hogy egy szaturnuszi nap hossza számottevően rövidebb az egyenlítője környékén, mint a sarkvidékek közelében. Ahol differenciális rotáció van, ott azonban "szélnyírás" is fellép, s ekkor bizony előfordulhat, hogy a szél, amely épp két különbözőképp forgó tartomány határán fúj, meanderezni, hullámozni kezd. Kis szerencsével előállhat olyan helyzet, hogy a szél-furóáramlás becakkosodásának hullámhossza éppen egész számszor férjen el a bolygó körül. Ehhez azonban sokmindennek passzolnia kell: a planéta méretének, a légkör vastagságának (bármit is jelentsen ez) és a forgási szögsebességnek egy finom kombinációja kellhet ahhoz, hogy éppen hatszögesen kanyargó áramlást kapjunk. De adottak-e ennek a feltételei a Szaturnuszon? Talán igen, de hogy megtudjuk, jól jön a jelenség "vizes" forgatott modellje.
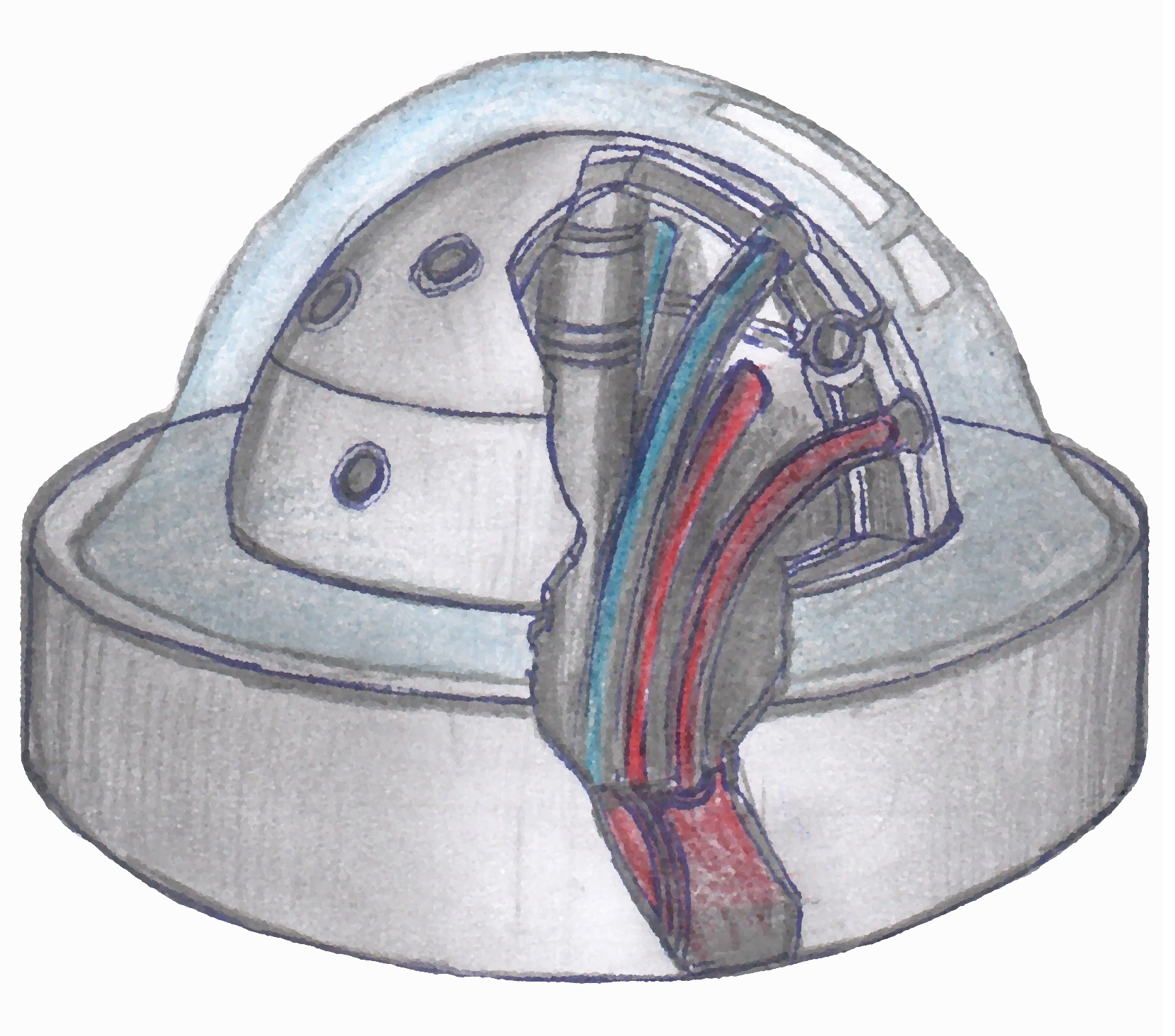
A rajzon látható, leginkább egy ufó-karikatúrájára emlékeztető szerkezet képes lenne arra, hogy egy félgömb alakú, de függetlenül forgó részekből álló műanyag felületre felcuppantott súlytalan vízcseppet úgy pörgessünk be, hogy az egyenlítői részét gyorsabban tekerjük, mint a sarkit, miközben a vízfelszín szabadon marad, s felületi feszültsége miatt igyekszik félgömb alakját megtartani. A vízben feloldott követőrészecske-szemcsék kamerás követésével szerencsés esetben kirajzolódhat az elmélet által jósolt hatszöges mintázat, mellyel erős bizonyítékát adhatnánk a szélnyírásos elmélet helyességének. Persze itt is, mint mindig, az ördög a részletekben bújik meg. De hogyan is jutna fel ez a szerkezet az űrbe és mi egyebet tanulhatnánk a DiRoS-tól, ha a repülés valóra válna? Kiderül az adásból. Hallgassátok szeretettel!
emTV.hu // cikk: Vincze Miklós // borítókép: NASA / Cassini // kép: Vincze Miklós, DiRoS